CaratheodoryPruning.jl Documentation

Carathéodory's theorem is a theorem in convex geometry relating to a minimal number of points in $\R^N$ required to enclose some point. Suppose that you have a set of points $P \in \mathbb{R}^N$ with $|P| > N$. Additionally, let $\mathbf{x} \in \text{conv}(P)$, the convex hull of $P$. This means that $\mathbf{x}$ can be written as a positive linear combination of the points in $P$ where the coefficients sum to one. The theorem states that there exists a subset $Q\subset P$ with $|Q|=N+1$ such that $\mathbf{x} \in \text{conv}(Q)$. In $N=2$ dimensions, this means that given some number of points that enclose $\mathbf{x}$, we can always prune these down to three points, or a triangle, that enclose $\mathbf{x}$.

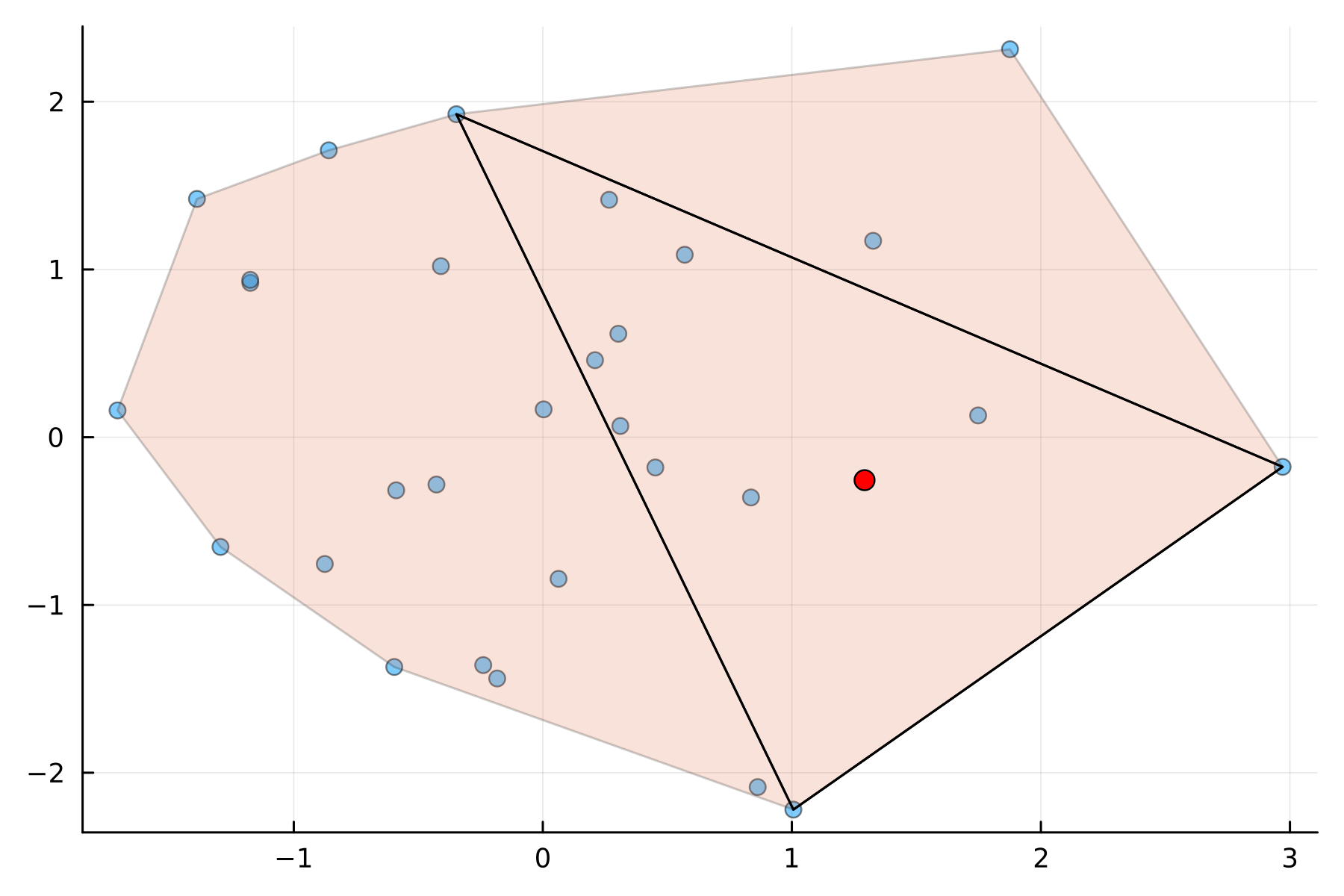
This theorem also extends to conic hulls, where the coefficients of the linear combination need not add to one, they simply need to be nonnegative. In the conic case, with $\mathbf{x} \in \text{cone}(P)$, the conic hull of $P$, there exists a subset $Q\subset P$ with $|Q|=N$ such that $\mathbf{x} \in \text{cone}(Q)$.

We can write out the conic version of Carathéodory's theorem as follows. Denote the points in $P$ as $\mathbf{p}_1, \ldots, \mathbf{p}_M$. Also define be the matrix

\[\mathbf{P} = \begin{bmatrix} \vert & \vert & & \vert\\ \mathbf{p}_1 & \mathbf{p}_2 & \cdots & \mathbf{p}_M\\ \vert & \vert & & \vert\\ \end{bmatrix} \in \mathbb{R}^{N \times M}.\]

The statement that $\mathbf{x}\in\text{cone}(P)$ implies that there exists a nonnegative vector of weights, $\mathbf{w} \in \mathbb{R}^M$, such that

\[\mathbf{P} \mathbf{w} = \mathbf{x}.\]

Carathéodory's theorem states that we can form a subset of points $Q \subset P$, such that we get a new set of nonnegative weights, $\mathbf{v}\in\mathbb{R}^{N}$, satisfying

\[\mathbf{Q} \mathbf{v} = \begin{bmatrix} \vert & \vert & & \vert\\ \mathbf{p}_{i_1} & \mathbf{p}_{i_2} & \cdots & \mathbf{p}_{i_N}\\ \vert & \vert & & \vert\\ \end{bmatrix} \mathbf{v} = \mathbf{x} = \mathbf{P} \mathbf{w}.\]

Once the row indices, $i_1, \ldots, i_N$, are sampled, we can obtain the new weights by performing a linear solve on the matrix equation $\mathbf{Q} \mathbf{v} = \mathbf{x}$. However, the difficulty in this problem is in subsampling the correct row indices such that the new weights are all nonnegative. The goal of having nonnegative weights can be useful in problems such as numerical quadrature where negative weights could lead to numerical instability.

CaratheodoryPruning.jl implements various algorithms for this row index subselection problem.

The base Carathéodory pruning method takes in a matrix V of size M by N, or the transpose of the $\mathbf{P}$ matrix above. It also takes in a vector of nonnegative weights w_in of length M. It then returns a nonnegative pruned vector, w, of length M, and a vector of row indices of length N, inds, such that V[inds,:]' * w[inds] is approximately equal to V' * w_in. If return_errors is set to true, it additionally returns a vector of moment errors at each iteration.

The implemented methods for Carathéodory pruning are iterative kernel-based algorithms. This means that at each step, kernel vectors for the transpose of V[inds,:] are formed so that they can be used to pivot the weights without changing the moments. The pivot is chosen to ensure that (at least) one of the weights are set to zero, and the rest are still nonnegative. This iteration is then repeated until M - N of the row indices are pruned, and we are left with N row indices.

Here is a full example of generating a random matrix V and random, positive vector of weights w_in, computing the moments eta, using caratheodory_pruning to generate pruned weights w, and computing the moment error.

using CaratheodoryPruning
using Random
M = 100
N = 10
V = rand(M, N)
w_in = rand(M)
eta = V' * w_in
w, inds = caratheodory_pruning(V, w_in)
w[inds]

10-element Vector{Float64}:
  6.024729738575634
  6.453835375942296
  3.929483809621981
  2.9016573147807136
  7.451269086546258
 14.833288666800724
  1.8868570997858618
  5.684190887232419
  0.5472984525001309
  5.739878063461836

error = maximum(abs.(V[inds,:]' * w[inds] .- eta))

1.7763568394002505e-14